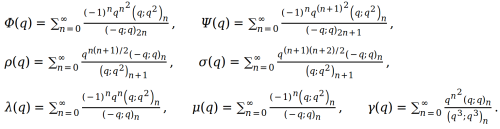શ્રીનિવાસ ઐયંગાર રામાનુજન
(તમિલ: ஸ்ரீனிவாஸ ஐயங்கார் ராமானுஜன்; ૨૨ ડિસેમ્બર ૧૮૮૭ – ૨૬ એપ્રિલ ૧૯૨૦) ૨૦મી સદીમાં ભારતના સૌથી મહાન અને સૌથી પ્રખ્યાત ગણિતજ્ઞ થઇ ગયા. નાનપણથીજ તેઓ ગણિતમાં અસાધારણ પ્રતિભા દેખાડી શિક્ષકોને અચંબામાં નાખી દેતા હતા. મુખ્યતઃ તેઓ ગણિત જાતે જ શિખ્યા હતા અને જીવનમાં ક્યારેય યુનિવર્સીટી ગયા નહોતા.
રામાનુજનની પ્રતિભાની ઓળખ વિશ્વને કરાવી રામાનુજનને પ્રસિદ્ધ કરવામાં અંગ્રેજ પ્રોફેસર ગૉડફ્રે હાર્ડિનો મોટો હાથ હતો.
તાજેતર માં ૨૨ ડિસેમ્બર ૨૦૧૨ ના રોજ તેમની ૧૫૦મી જન્મતિથિ ઉજવવામા આવી હત
Srinivasa Ramanujan (1887—1920)
Ramanujan was one of the greatest mathematical geniuses ever to emerge from India. Born into a poor Brahmin family, he had limited formal education. At age 15, he was given a copy of Carr’s Synopsis of Pure Mathematics. Through this book, Ramanujan “went ranging with delight”. He set out to prove all the results in the book.
Consumed by his passion for mathematics, Ramanujan neglected all other subjects. As a result, he failed the entrance exam for the University of Madras. However, he continued his mathematical research with intensity and, by his early twenties, had become known to the leading mathematicians in the region.
In 1913, Ramanujan wrote to G H Hardy, the leading mathematician in Britain, enclosing a list of about 120 mathematical results. Hardy examined the results and recognised that, while some of them were well known, others were profoundly original and “could only be written down by a mathematician of the highest class”.
 The
collaboration between Hardy and Ramanujan was among the most successful
mathematical collaborations of all time. They published many papers of
great originality. In 1918 Ramanujan was elected a Fellow of the Royal
Society. In the same year he became a Fellow of Trinity College
Cambridge.
The
collaboration between Hardy and Ramanujan was among the most successful
mathematical collaborations of all time. They published many papers of
great originality. In 1918 Ramanujan was elected a Fellow of the Royal
Society. In the same year he became a Fellow of Trinity College
Cambridge.
Ramanujan was dogged by poor health. He lived for only one year after his return to India in 1919, but, during this year, he discovered a completely new species of mathematical objects, which he called mock theta functions. They were mentioned in a last letter to Hardy, and many results concerning them are in a set of papers sent to Hardy after Ramanujan’s death.
The Lost Notebook
In 1976 the American mathematician George Andrews was looking through a box of papers in the Wren Library in Cambridge and found what is now known as the “Lost Notebook”. It included Ramanujan’s results on the mysterious mock theta functions.
Andrews’ discovery opened up a vast new landscape. The results were of stunning novelty and huge significance, representing what many regard as Ramanujan’s deepest work, and confirming Hardy’s earlier description of Ramanujan as having “profound and invincible originality”.
The finding of the lost notebook has been compared to opening a box and finding a manuscript of Beethoven’s Tenth Symphony. The consequences have been profound, and there remains much yet to be discovered, in both mathematics and physics, arising from this startlingly brilliant work.
Mock Theta Functions
The discovery of the lost notebook triggered an explosion of research. The mock theta functions are now understood in the broader perspective of structures called Modular Forms. Technically, modular forms are holomorphic functions on the upper half complex plane. They are defined on lattices in the complex plane, and satisfy certain crucial transformation properties. Modular forms played a key role in Wiles’ proof of Fermat’s last theorem.
Ramanujan’s mock theta functions (MTFs) are similar to, but more general than the classical theta functions of Jacobi. A full chapter of Whittaker and Watson’s classical text, Modern Analysis, is devoted to Jacobi’s functions. Theta functions are essentially complex extensions of trigonometric functions, elliptic analogues of the exponential function. They are quasi-doubly periodic functions.
In a brilliant doctoral thesis, the Dutch mathematician Sander Zwegers, who worked at UCD before moving to Cologne in 2011, clarified the nature of the mock theta functions: He found that the MTFs had to be completed by adding to them a non-holomorphic function called a period integral. He showed how each MTF could be expressed as the holomorphic part of a real modular form. Zwegers also produced infinite families of MTFs, greatly extending Ramanujan’s discovery.
Applications
The breakthrough in our understanding of the nature of the mock theta functions is having an impact on many areas of mathematics and physics. In pure mathematics, the results have been applied to the theory of partitions, group theory and the differential topology of the complex plane.
In the 1970s, a surprising connection between the largest sporadic finite simple group, called the Monster, and classical elliptic modular functions was found. The generalization of this discovery led to what John Conway called “Monster Moonshine”. Now, similar connections have been found involving MTFs. The coefficients of these functions are related to the representation of some of the sporadic (finite simple) groups such as M24.
In physics, the connection has led to applications in several areas: particle physics, statistical mechanics, polymer chemistry, computer science and cosmology. In the last of these areas, MTFs have found to be valuable for calculating the entropy of black holes.
Conclusion
At the Ramanujan Conference in 1987, referring to the mock theta functions, mathematician and theoretical physicist Freeman Dyson spoke of “a grand synthesis still to be discovered”, and he speculated about their application to physics in the context of string theory. He concluded that “the mock theta functions give us tantalizing hints of a grand synthesis, still to be discovered”.
This is an indication of the prescience and genius of Ramanujan. Many mathematicians are very excited that results discovered by Ramanujan almost one hundred years ago are now such hot topics.
(તમિલ: ஸ்ரீனிவாஸ ஐயங்கார் ராமானுஜன்; ૨૨ ડિસેમ્બર ૧૮૮૭ – ૨૬ એપ્રિલ ૧૯૨૦) ૨૦મી સદીમાં ભારતના સૌથી મહાન અને સૌથી પ્રખ્યાત ગણિતજ્ઞ થઇ ગયા. નાનપણથીજ તેઓ ગણિતમાં અસાધારણ પ્રતિભા દેખાડી શિક્ષકોને અચંબામાં નાખી દેતા હતા. મુખ્યતઃ તેઓ ગણિત જાતે જ શિખ્યા હતા અને જીવનમાં ક્યારેય યુનિવર્સીટી ગયા નહોતા.
રામાનુજનની પ્રતિભાની ઓળખ વિશ્વને કરાવી રામાનુજનને પ્રસિદ્ધ કરવામાં અંગ્રેજ પ્રોફેસર ગૉડફ્રે હાર્ડિનો મોટો હાથ હતો.
તાજેતર માં ૨૨ ડિસેમ્બર ૨૦૧૨ ના રોજ તેમની ૧૫૦મી જન્મતિથિ ઉજવવામા આવી હત
Srinivasa Ramanujan (1887—1920)
Ramanujan was one of the greatest mathematical geniuses ever to emerge from India. Born into a poor Brahmin family, he had limited formal education. At age 15, he was given a copy of Carr’s Synopsis of Pure Mathematics. Through this book, Ramanujan “went ranging with delight”. He set out to prove all the results in the book.
Consumed by his passion for mathematics, Ramanujan neglected all other subjects. As a result, he failed the entrance exam for the University of Madras. However, he continued his mathematical research with intensity and, by his early twenties, had become known to the leading mathematicians in the region.
In 1913, Ramanujan wrote to G H Hardy, the leading mathematician in Britain, enclosing a list of about 120 mathematical results. Hardy examined the results and recognised that, while some of them were well known, others were profoundly original and “could only be written down by a mathematician of the highest class”.

Left: Indian postage stamp issued in 1962, the 75th anniversary of Ramanujan’s birth. Right: G H Hardy.
Ramanujan was dogged by poor health. He lived for only one year after his return to India in 1919, but, during this year, he discovered a completely new species of mathematical objects, which he called mock theta functions. They were mentioned in a last letter to Hardy, and many results concerning them are in a set of papers sent to Hardy after Ramanujan’s death.
The Lost Notebook
In 1976 the American mathematician George Andrews was looking through a box of papers in the Wren Library in Cambridge and found what is now known as the “Lost Notebook”. It included Ramanujan’s results on the mysterious mock theta functions.
Andrews’ discovery opened up a vast new landscape. The results were of stunning novelty and huge significance, representing what many regard as Ramanujan’s deepest work, and confirming Hardy’s earlier description of Ramanujan as having “profound and invincible originality”.
The finding of the lost notebook has been compared to opening a box and finding a manuscript of Beethoven’s Tenth Symphony. The consequences have been profound, and there remains much yet to be discovered, in both mathematics and physics, arising from this startlingly brilliant work.
Mock Theta Functions
The discovery of the lost notebook triggered an explosion of research. The mock theta functions are now understood in the broader perspective of structures called Modular Forms. Technically, modular forms are holomorphic functions on the upper half complex plane. They are defined on lattices in the complex plane, and satisfy certain crucial transformation properties. Modular forms played a key role in Wiles’ proof of Fermat’s last theorem.
Ramanujan’s mock theta functions (MTFs) are similar to, but more general than the classical theta functions of Jacobi. A full chapter of Whittaker and Watson’s classical text, Modern Analysis, is devoted to Jacobi’s functions. Theta functions are essentially complex extensions of trigonometric functions, elliptic analogues of the exponential function. They are quasi-doubly periodic functions.
In a brilliant doctoral thesis, the Dutch mathematician Sander Zwegers, who worked at UCD before moving to Cologne in 2011, clarified the nature of the mock theta functions: He found that the MTFs had to be completed by adding to them a non-holomorphic function called a period integral. He showed how each MTF could be expressed as the holomorphic part of a real modular form. Zwegers also produced infinite families of MTFs, greatly extending Ramanujan’s discovery.
Applications
The breakthrough in our understanding of the nature of the mock theta functions is having an impact on many areas of mathematics and physics. In pure mathematics, the results have been applied to the theory of partitions, group theory and the differential topology of the complex plane.
In the 1970s, a surprising connection between the largest sporadic finite simple group, called the Monster, and classical elliptic modular functions was found. The generalization of this discovery led to what John Conway called “Monster Moonshine”. Now, similar connections have been found involving MTFs. The coefficients of these functions are related to the representation of some of the sporadic (finite simple) groups such as M24.
In physics, the connection has led to applications in several areas: particle physics, statistical mechanics, polymer chemistry, computer science and cosmology. In the last of these areas, MTFs have found to be valuable for calculating the entropy of black holes.
Conclusion
At the Ramanujan Conference in 1987, referring to the mock theta functions, mathematician and theoretical physicist Freeman Dyson spoke of “a grand synthesis still to be discovered”, and he speculated about their application to physics in the context of string theory. He concluded that “the mock theta functions give us tantalizing hints of a grand synthesis, still to be discovered”.
This is an indication of the prescience and genius of Ramanujan. Many mathematicians are very excited that results discovered by Ramanujan almost one hundred years ago are now such hot topics.